Нечеткая арифметика

В этом разделе рассматриваются способы расчета значений четких алгебраических функций от нечетких аргументов. Материал основывается на понятиях нечеткого числа и принципа нечеткого обобщения. В конце раздела приводятся правила выполнения арифметических операций над нечеткими числами.

Определение 25. Нечетким числом называется выпуклое нормальное нечеткое множество с кусочно-непрерывной функцией принадлежности, заданное на множестве действительных чисел. Например, нечеткое число «около 10» можно задать следующей функцией принадлежности:

.

Определение 26. Нечеткое число называется положительным (отрицательным) если , ().

Определение 27. Принцип обобщения Заде. Если - функция от n независимых переменных и аргументы заданы нечеткими числами , соответственно, то значением функции называется нечеткое число с функцией принадлежности:

.

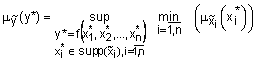Принцип обобщения позволяет найти функцию принадлежности нечеткого числа, соответствующего значения четкой функции от нечетких аргументов. Компьютерно-ориентированная реализация принципа нечеткого обобщения осуществляется по следующему алгоритму:

Шаг 1. Зафиксировать значение .

Шаг 2. Найти все n-ки , , удовлетворяющие условиям и , .

Шаг 3. Степень принадлежности элемента нечеткому числу вычислить по формуле: .

Шаг 4. Проверить условие «Взяты все элементы y?». Если «да», то перейти к шагу 5. Иначе зафиксировать новое значение и перейти к шагу 2.

Шаг 5. Конец.

Приведенный алгоритм основан на представлении нечеткого числа на дискретном универсальном множестве, т.е. 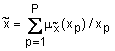. Обычно исходные данные , задаются кусочно-непрерывными функциями принадлежности: . Для вычисления значений функции аргументы , дискретизируют, т.е. представляют в виде 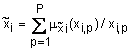. Число точек выбирают так, чтобы обеспечить требуемую точность вычислений. На выходе этого алгоритма получается нечеткое множество, также заданное на дискретном универсальном множестве. Результирующую кусочно-непрерывную функцию принадлежности нечеткого числа получают как верхнюю огибающую точек .

Интересное из раздела

Особенности формирования и реализация ценовой политики предприятия в условиях переходного периода
ценовая политика государственный переходной Ключевыми элементами рыночной экономики являются цены, ценообразование и ценовая политика предприятия. Цена - это экономическая категория, означающа ...

Оценка кредитоспособности энергетической компании
В последние годы ярко выраженной тенденцией в банковском деле становится развитие кредитных операций с юридическими лицами, предпринимателями и населением. В связи с этим существенно повышается ур ...

Открытое акционерное общество Дом
Бизнес-план - это документ, содержащий основные аспекты будущего коммерческого начинания. В нем анализируются проблемы, с которыми предприниматель может встретиться, а также определяются способы ...